Bir program kodunun zaman karmaşıklığını hesaplamak için 5 kural
1 Döngüler
2 İç içe Döngüler
3 Ardışık deyimler
4 If-then-else deyimleri
5 Logaritmik karmaşıklık
KURAL 1: DÖNGÜLER
Bir döngünün çalışma zamanı en çok döngü içindeki deyimlerin çalışma zamanının iterasyon sayısıyla çarpılması kadardır.
for (i=1; i<=n; i++)
{
m = m + 2;
}
Toplam zaman = sabit c * n = cn = O(N)
KURAL 2: İÇ İÇE DÖNGÜLER
İçteki analiz yapılır. Toplam zaman bütün döngülerin çalışma sayılarının çarpımına eşittir
for (i=1; i<=n; i++) {
for (j=1; j<=n; j++) {
k = k+1;
}
}
Toplam zaman = c * n * n * = cn2 = O(N2)
KURAL 3: ARDIŞIK DEYİMLER
Her deyimin zamanı birbirine eklenir
x = x +1;
for (i=1; i<=n; i++) {
m = m + 2;
}
for (i=1; i<=n; i++) {
for (j=1; j<=n; j++) {
k = k+1;
}
}
toplam zaman = c0 + c1n + c2n2 = O(N2)
KURAL 4: IF-THEN-ELSE DEYİMLERİEn kötü çalışma zamanı:test zamanına then veya else kısmındaki çalışma zamanının hangisi büyükse o kısım eklenir.
if (depth( ) != otherStack.depth( ) ) {
return false;
}
else {
for (int n = 0; n < depth( ); n++) {
if (!list[n].equals(otherStack.list[n]))
return false;
}
}
Toplam zaman = c0 + c1 + (c2 + c3) * n = O(N)
KURAL 5: LOGARİTMİK KARMAŞIKLIK
Problemin büyüklüğünü belli oranda(genelde ½)
azaltmak için sabit bir zaman harcanıyorsa bu algoritma O(log N)’dir.
Örnek algoritma (binary search):
N sayfalı bir sözlükten bir sözcük arama
Sözlüğün orta kısmına bakılır
Sözcük ortaya göre sağda mı solda mı kaldığı bulunur?
Bu işlem sağ veya solda sözcük bulunana kadar tekrarlanır
O Notasyonu - Örnek 13n2+2n+5 = O(n2) ifadesinin doğru olup olmadığını ispatlayınız.
10 n2 = 3n2 + 2n2 + 5n2
3n2 + 2n + 5 for n 1
c = 10, n0 = 1
O Notasyonu - Örnek 2T(N)=O(7n2+5n+4) olarak ifade edilebiliyorsa, T(N) fonksiyonu aşağıdakilerden herhangi biri olabilir.
T(N)=n2
T(N)=1000n2+2n+300
T(N)= O(7n2+5n+4) =O(n2)
O Notasyonu - Örnek 3
Fonksiyonların harcadıkları zamanları O notasyonuna göre yazınız.
f1(n) = 10 n + 25 n2
f2(n) = 20 n log n + 5 n
f3(n) = 12 n log n + 0.05 n2
f4(n) = n1/2 + 3 n log n
 Algoritma, belli bir problemi çözmek veya belirli bir amaca ulaşmak için tasarlanan yol. Matematikte ve bilgisayar biliminde
bir işi yapmak için tanımlanan, bir başlangıç durumundan başladığında,
açıkça belirlenmiş bir son durumunda sonlanan, sonlu işlemler kümesidir.
Genellikle bilgisayar programlamada kullanılır ve tüm programlama
dillerinin temeli algoritmaya dayanır. Aynı zamanda algoritma tek bir
problemi çözecek davranışın, temel işleri yapan komutların veya
deyimlerin adım adım ortaya konulmasıdır ve bu adımların sıralamasına
dikkat edilmelidir. Bir problem çözülürken algoritmik ve sezgisel
(herustic) olmak üzere iki yaklaşım vardır. Algoritmik yaklaşımda da
çözüm için olası yöntemlerden en uygun olan seçilir ve yapılması
gerekenler adım adım ortaya konulur. Algoritmayı belirtmek için ;
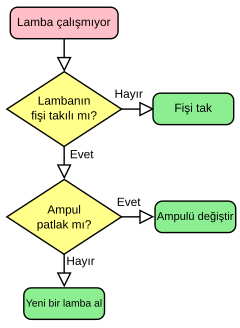
metinsel olarak düz ifade ve akış diyagramı olmak üzere 2 yöntem
kullanılır. Algoritmalar bir programlama dili vasıtasıyla bilgisayarlar tarafından işletilebilirler.
Algoritma, belli bir problemi çözmek veya belirli bir amaca ulaşmak için tasarlanan yol. Matematikte ve bilgisayar biliminde
bir işi yapmak için tanımlanan, bir başlangıç durumundan başladığında,
açıkça belirlenmiş bir son durumunda sonlanan, sonlu işlemler kümesidir.
Genellikle bilgisayar programlamada kullanılır ve tüm programlama
dillerinin temeli algoritmaya dayanır. Aynı zamanda algoritma tek bir
problemi çözecek davranışın, temel işleri yapan komutların veya
deyimlerin adım adım ortaya konulmasıdır ve bu adımların sıralamasına
dikkat edilmelidir. Bir problem çözülürken algoritmik ve sezgisel
(herustic) olmak üzere iki yaklaşım vardır. Algoritmik yaklaşımda da
çözüm için olası yöntemlerden en uygun olan seçilir ve yapılması
gerekenler adım adım ortaya konulur. Algoritmayı belirtmek için ;
metinsel olarak düz ifade ve akış diyagramı olmak üzere 2 yöntem
kullanılır. Algoritmalar bir programlama dili vasıtasıyla bilgisayarlar tarafından işletilebilirler.